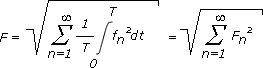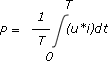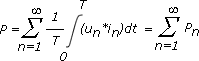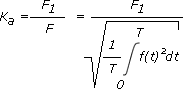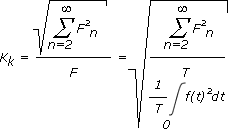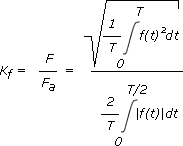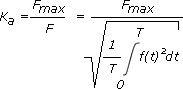Zusatzinfo |
|||||||||||||||||||||||||||||||||
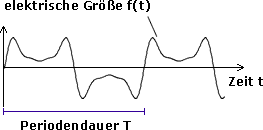
FourierzerlegungViele elektrische Wechselgrößen weichen mehr oder weniger stark von der idealen Sinusform ab. Um diese Größen trotzdem mathematisch beschreiben zu können, werden sie in eine Summe von sinusförmigen Einzelgrößen zerlegt. Addiert man zu jedem Zeitpunkt die Einzelgrößen, so erhält man wieder die ursprüngliche Größe. Das mathematische Verfahren, das diese Zerlegung ermöglicht, wird Fourierzerlegung genannt. Die folgende Gleichung gibt den Ansatz der Fourierzerlegung an:
Dabei sind:
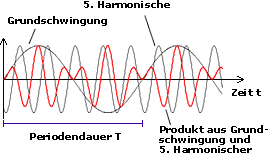
Die Funktion f(t) wird also aus einem Gleichanteil, einer Grundschwingung
und Vielfachen der Grundschwingung "zusammengesetzt". Die
Vielfachen der Grundschwingung werden auch als Oberschwingungen oder
Harmonische bezeichnet.
Mit den Zusammenfassungen
lässt sich schreiben:
Damit können periodische Größen auf zwei Arten dargestellt werden:
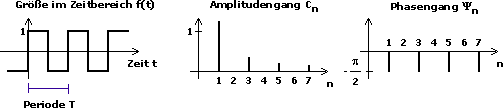
Das folgende Bild zeigt die Darstellung für ein Rechtecksignal im Zeit- und Frequenzbereich.
Die Fourier-Reihe für f(t) lautet:
Wie man sieht, nehmen die Koeffizienten Cn mit zunehmender Frequenz stark ab, so daß die Reihenentwicklung nach wenigen Summanden abgebrochen werden kann. Sehr hochfrequente Anteile werden im allgemeinen vernachlässigt.
Fourierzerlegung bei netzharmonische VorgängenBei netzharmonischen Vorgängen ergeben sich aufgrund ihrer Entstehung und der Gesetzmäßigkeiten des Drehstromnetzes Vereinfachungen im Amplituden- und Frequenzgang.
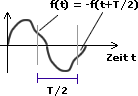
Symmetrie bezüglich der Zeitachse
f(t) = -f(t+T/2) Unter diesen Bedingungen verschwindet der Gleichanteil C0 und es treten nur Werte für Cn bei ungeradzahligem n auf. Eine solche Größe enthält also nur ungeradzahlige Vielfache der Grundschwingung bzw. der Netzfrequenz.
Symmetrisches Drehstromnetz
IL1 + IL2 + IL3 = 0 Unter diesen Bedingungen verschwinden alle Werte für Cn bei denen n durch 3 teilbar ist. Ursache dafür ist, dass die Summe der durch 3 teilbaren Oberschwingungen nicht 0 ergeben würde. Damit können sich diese Oberschwingungen im Strom nicht ausprägen. Das nachfolgende Bild zeigt die zeitlichen Verläufe.
Da keine Ströme entsprechender Frequenz fließen können,
treten an den Leitungsimpedanzen auch keine Spannungsabfälle mit
durch 3 teilbarer Oberschwingungsfrequenz auf. Frequenzspektren von oberschwingungsbehafteten Strömen und Spannungen enthalten in symmetrischen Drehstromnetzen deshalb nur die Grundschwingung sowie die 5., 7., 11., 13., 17., 19. ... Oberschwingung. Hinweis: Ein Drehstromnetz, bei dem Ströme über den geerdeten Sternpunkt des Netztransformators fließen, ist nicht mehr symmetrisch.
Effektivwert nichtsinusförmiger periodischer GrößenDer Effektivwert F einer periodischen Größe ist definiert als:
Die Funktion f(t) wird nun durch ihre Darstellung als Fourierreihe f(t) = f1 + f2 + f3 + ... ersetzt. f(t)² = (f1 + f2 + f3 + ...)*(f1 + f2 + f3 + ...) = f1² + f1f2 + f1f3 +...+ f2² + f2f1 + f2f3 +... und nach Einsetzen in die Definitionsgleichung für F:
Wirkleistung nichtsinusförmiger periodischer GrößenDie Wirkleistung P einer periodischen Größe ergibt sich als Mittelwert der Leistung über eine Periode T:
Strom und Spannung sind nichtsinusförmige Größen und werden dementsprechend durch ihre Fourierreihen beschrieben:
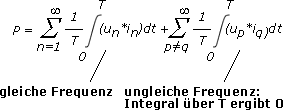
Für u*i ergibt sich damit: u*i= (u1 + u2 + u3 + ...)*(i1 + i2 + i3 + ...) = u1*i1 + u1*i2 + u1*i3 +...+ u2*i1 + u2*i2 + u2*i3 + ... und nach Einsetzen in die Definitionsgleichung für P:
Bildet man die Integrale für alle Produkte up*iq über die Periodendauer T, so verschwinden die Integrale für die Produkte aus ungleichen Frequenzanteilen. Für die Berechnung der Wirkleistung müssen also nur die Produkte gleicher Frequenzanteile von u und i berücksichtigt werden. Damit ergibt sich für die Wirkleistung P:
Die Wirkleistung ist damit gleich der Summe aus der Wirkleistung für die Grundschwingung und jeder Harmonischen.
Weitere Kennwerte periodischer GrößenPeriodische Größen werden neben ihrer Darstellung im Zeit- und Frequenzbereich durch weitere Kennwerte beschrieben. Diese geben an, wie stark die periodische Größe von einer idealen Sinusform abweicht.
|
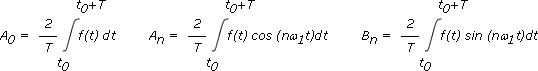
 Netzharmonische
Vorgänge sind oft bezüglich der Zeitachse symmetrisch. Das heißt:
Netzharmonische
Vorgänge sind oft bezüglich der Zeitachse symmetrisch. Das heißt: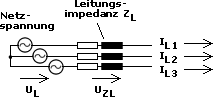 Für
eine symmetrisches Drehstromnetz ist die Summe der Phasenströme gleich
Null.
Für
eine symmetrisches Drehstromnetz ist die Summe der Phasenströme gleich
Null. 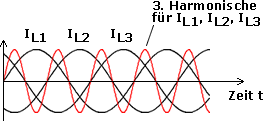 Wie
zu erkennen ist, fallen die durch 3 teilbaren Harmonischen genau übereinander
und heben sich in ihrer Summe nicht auf.
Wie
zu erkennen ist, fallen die durch 3 teilbaren Harmonischen genau übereinander
und heben sich in ihrer Summe nicht auf.
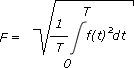
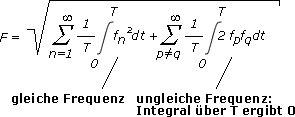
 Bildet
man die Integrale für alle Produkte fpfq über die Periodendauer T, so verschwinden die Integrale für
die Produkte aus ungleichen Frequenzanteilen. Für die Berechnung
des Effektivwertes müssen also nur die Quadrate fn² aller Frequenzanteile von f(t) berücksichtigt werden. Damit
ergibt sich für den Effektivwert F der Funktion f(t):
Bildet
man die Integrale für alle Produkte fpfq über die Periodendauer T, so verschwinden die Integrale für
die Produkte aus ungleichen Frequenzanteilen. Für die Berechnung
des Effektivwertes müssen also nur die Quadrate fn² aller Frequenzanteile von f(t) berücksichtigt werden. Damit
ergibt sich für den Effektivwert F der Funktion f(t):