Zusatzinfo |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Herleitung des optimalen ÜbersetzungsverhältnissesUmrechnung des Drehmomentes
Für diesen Fall ergibt sich aus dem Energieerhaltungssatz, dass die vom Antrieb eingespeiste Energie gleich der sein muss, die das Getriebe an seinem Abtrieb abgibt. Man kann deshalb schreiben:
Daraus ergibt sich für t1=t2:
Das Übersetzungsverhältnis bestimmt damit auch das Drehmoment, das am Abtrieb wirksam wird. Da üblicher Weise i>1 ist, ist das abgegebene Drehmoment größer als das vom Motor eingespeiste Drehmoment. In der überwiegenden Mehrzahl reduziert das rotatorische Getriebe in seiner Funktion als Kenngrößenwandler die Motordrehzahl und vergrößert das Motordrehmoment.
Lastbeschleunigung und ÜbersetzungsverhältnisDie allgemeine Gleichung zur Drehmomentbilanz lautet:
mit J1: Trägheitsmoment des Motors Unter Berücksichtigung des oben dargestellten Zusammenhanges zwischen antriebs- und abtriebsseitigen Drehmomenten lässt sich die Gleichung umformen zu:
mit J2: Trägheitsmoment der Last Ersetzt man nun noch ω1 mit Hilfe des Übersetzungsverhältnisses, ergibt sich:
Damit ist der Zusammenhang zwischen dem Motordrehmoment und der Lastbeschleunigung gegeben. Für
wird bei einer vom Prozess geforderten Lastbeschleunigung dω2/dt das erforderliche Motordrehmoment minimal. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
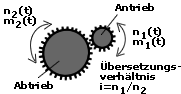 Der
Antrieb speist ein Drehmoment m1 in das Getriebe
ein. Das Getriebe stellt an seinem Abtrieb das Drehmoment m2 bereit. Dieses wird durch ein angreifendes Lastmoment kompensiert. Antrieb
und Getriebe führen eine gleichmäßige Drehbewegung aus.
Der
Antrieb speist ein Drehmoment m1 in das Getriebe
ein. Das Getriebe stellt an seinem Abtrieb das Drehmoment m2 bereit. Dieses wird durch ein angreifendes Lastmoment kompensiert. Antrieb
und Getriebe führen eine gleichmäßige Drehbewegung aus.