Experimentieren Sie mit virtuellen Testständen im:



Legen Sie Antriebe aus mit:

Auslegung elektrischer Antriebe

 

Mechanische Motorauslegung

Ermittlung des Motordrehmomentes

Das Drehmoment, das der Motor an seiner Welle bereitstellt, hat zwei Funktionen. Es dient

• zur Beschleunigung bzw. Verzögerung der mechanischen Elemente in der Arbeitsmaschine und
• zur Kompensation der auftretenden Lastmomente.

In praktischen Anwendungen sind im allgemeinen mehrere mechanische Elemente an den Bewegungsabläufen beteiligt und die Lastmomente werden an verschiedenen Punkten des mechanischen Systems wirksam. Um die Komplexität zu verringern, ist es zweckmäßig, das mechanische System in Teilsysteme zu zerlegen und jedes Teilsystem separat zu betrachten. Damit ergibt sich das nebenstehende Modell für das mechanische System, das an den Motor angekoppelt ist.

Es ist durchaus möglich, dass ein Teilsystem nochmals in Untersysteme zerlegt werden muss.

Dabei sind:

M0,1,2,...	Drehmoment am Antriebspunkt des Teilsystems. Dieses Drehmoment wird am vorgelagerten Teilsystem als zusätzliches Lastmoment wirksam
ML0,1,2,...	Lastmoment im Teilsystem
J0,1,2,...	Trägheitsmoment des Teilsystems
ω0,1,2,...	Winkelgeschwindigkeit des Teilsystems
i1,2,...	Übersetzungsverhältnis des Teilsystems

Hinweis:
Im Trägheitsmoment J0 ist die Trägheit des Motors nicht enthalten. Diese ist erst bekannt, wenn ein Motor ausgewählt wurde. Es muss später in einer "Nachrechnung" berücksichtigt werden.

Mit diesem Ansatz ergibt sich für das Drehmoment, das der Motor an seiner Welle bereitstellen muss, folgende Gleichung:

M0	=	Mb0		+	ML0		+	M1/i1
Drehmoment, das der Motor an seiner Welle bereitstellen muss		Beschleunigungsmoment für die an der Motorwelle gekoppelte Trägheit			Lastmoment, das an der Motorwelle angreift			Drehmoment, das an das vorgelagerte mechanische Teilsystem übertragen wird

mit den Teilgleichungen:

Mb0	=	J0*(dω0/dt)
M1	=	J1*(dω1/dt)		+	ML1		+	M2/i2
M2	=	J2*(dω2/dt)		+	ML2		+	M3/i3
...

Das Drehmoment, das der Motor an seiner Welle bereitstellen muss, kann damit schrittweise beginnend mit dem letzten Teilsystem in der Wirkkette berechnet werden.

In der praktischen Anwendung kommt es drauf an, die Teilsysteme eindeutig zu erkennen und die wirksamen Übersetzungsfaktoren richtig zu ermitteln. Besonders bei der Wandlung linearer in rotatorische Bewegungen können die Zusammenhänge relativ komplex sein. Oft sind jedoch Vereinfachungen möglich, die die Berechnung erleichtern.

Bei den auftretenden Lastmomenten spielt die Reibung eine besondere Rolle. Durch Reibung wird mechanische Energie in Wärme umgewandelt. Das heißt, dass das Reibmoment innerhalb eines mechanischen Systems immer in die gleiche Richtung wirkt wie die aktuelle Drehzahl bzw. Geschwindigkeit im Teilsystem. Ändert sich innerhalb des Lastspiels die Drehrichtung, ändert sich auch die Richtung des Reibmomentes.
In der Berechnung des erforderlichen Motordrehmomentes führt die Reibung während des motorischen Betriebs (z.B. beim Beschleunigen) zu einer Erhöhung und im generatorischen Betrieb (z.B. beim Bremsen) zu einer Absenkung des erforderlichen Motordrehmomentes.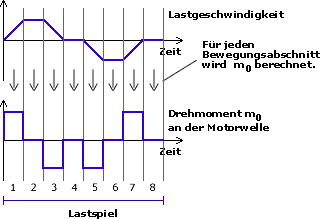

Für jeden Bewegungsabschnitt muss das Drehmoment m0 berechnet werden. Dieser Vorgang ist je nach Anzahl und Komplexität der Teilsysteme mit einem gewissen Aufwand verbunden. Das ist insbesondere dann der Fall, wenn die auftretenden Lastmomente nicht konstant sondern zeitlich veränderlich sind oder von der augenblicklichen Geschwindigkeit bzw. Drehzahl abhängen. Die mechanische Reibung, die in vielen Anwendungen nicht vernachlässigt werden kann, stellt ein solches veränderliches Lastmoment dar.

Nach der Berechnung und Addition aller Teildrehmomente in allen Bewegungsabschnitten liegt das nebenstehende Diagramm vor. Aus ihm kann der zeitliche Verlauf des vom Motor bereitzustellenden Drehmomentes m0 abgelesen werden. Gemeinsam mit dem Drehzahlverlauf an der Motorwelle liefert es die benötigten Kennwerte zur Auswahl des Motors.