Experimentieren Sie mit virtuellen Testständen im:



Legen Sie Antriebe aus mit:

Regelverfahren für elektrische Antriebe

 

Stromregelung für Asynchronmotoren

Koordinatensysteme

Asynchronmotoren sind 3-phasig aufgebaut und werden mit sinusförmigen Eingangsgrößen betrieben. Dadurch ergeben sich komplexe Zusammenhänge, die durch die vektorielle Beschreibung vereinfacht werden.
Vektorielle Größen sind jeweils für ein bestimmtes Koordinatensystem definiert. In diesem Koordinatensystem werden sie durch zwei rechtwinklig zueinander stehende Komponenten (Real- und Imaginärteil) beschrieben.

Im Gegensatz zu Synchronmotoren verfügen Asynchronmotoren über drei Koordinatensysteme - ein ständerfestes, ein synchron umlaufendes und ein läuferfestes Koordinatensystem.
Das ständerfeste Koordinatensystem ist auf die Wicklungen des Ständers orientiert und unbeweglich. Seine beiden Achsen werden mit den griechischen Buchstaben "α" und "β" bezeichnet. Von hoher Bedeutung ist das synchron umlaufende Koordinatensystem. Seine Achsen tragen die Bezeichnungen "d" und "q". Dieses Koordinatensystem rotiert mit der Frequenz der speisenden Spannung. Die d-Achse des synchronen Koordinatensystems ist auf den Läuferfluss ausgerichtet. Man spricht deshalb auch vom feldorientierten Koordinatensystem. Für eine mathematisch korrekte Darstellung erfolgt die Rotation im mathematisch positiven Sinn, also entgegen dem Uhrzeigersinn.
Das läuferfeste Koordinatensystem ist mit dem Läufer des Asynchronmotors verbunden und rotiert mit diesem. Aufgrund der asynchronen Rotation des Läufers fällt dieses Koordinatensystem nicht mit dem synchronen Koordinatensystem zusammen, wie es beim Synchronmotor der Fall ist. Für die regelungstechnische Betrachtung ist das läuferfeste Koordinatensystem jedoch von untergeordneter Bedeutung. Es wird deshalb nachfolgend nicht weiter behandelt.

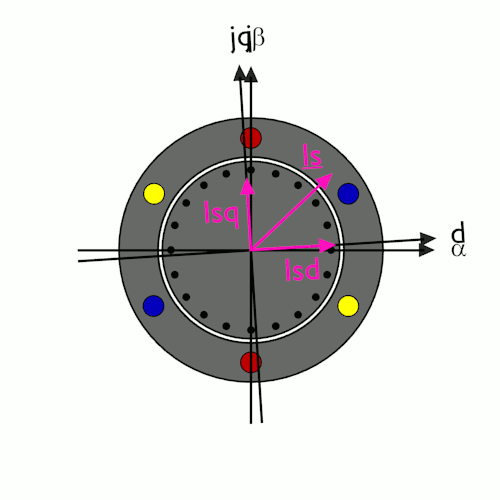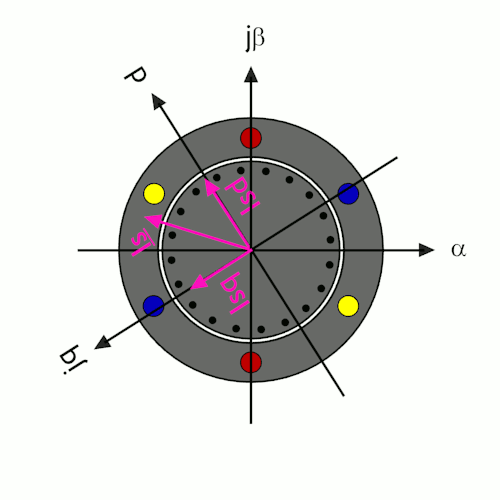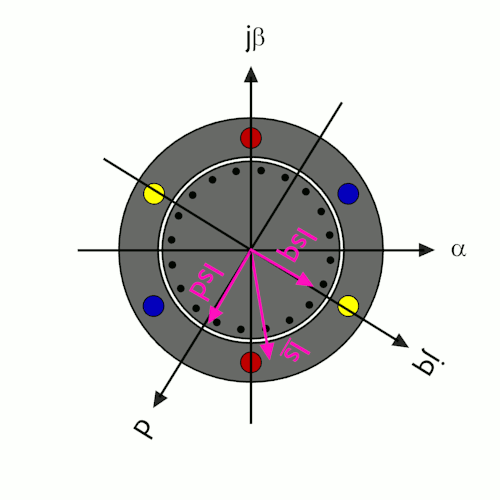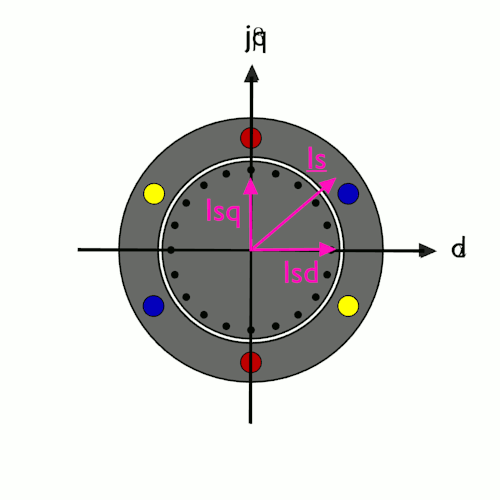
Betrachtet man die elektrischen Größen eines Asynchronmotors in den verschiedenen Koordinatensystemen, so ergibt sich ein interessanter Effekt. Im ständerfesten Koordinatensystem rotieren die Vektoren und die α- und β-Komponenten des Strom- und des Spannungszeigers weisen sinusförmige Verläufe auf. Wechselt man jedoch in das feldorientierte Koordinatensystem, scheinen Strom- und Spannungszeiger stillzustehen, da sie mit der gleichen Geschwindigkeit umlaufen wie das feldorientierte Koordinatensystem selbst. Die d- und q-Komponenten des Strom- und des Spannungszeigers werden im feldorientierten Koordinatensystem zu Gleichgrößen, was die regelungstechnische Behandlung stark vereinfacht. Aus diesem Grund erfolgt auch die Stromregelung des Asynchronmotor im feldorientierten Koordinatensystem. Diese Vereinfachung erfordert jedoch einen hohen Rechenaufwand für die Übertragung der elektrischen Messgrößen Strom- und Spannung in das bzw. aus dem feldorientierten Koordinatensystem. Im Vergleich zum Synchronmotor entsteht noch zusätzlicher Aufwand dadurch, dass die augenblickliche Lage des feldorientierten Koordinatensystems nicht über die Lage des Läufers einfach gemessen werden kann sondern fortlaufend berechnet werden muß. Deshalb ist die "vektoriellen Regelung" von Asynchronmotoren ausschließlich digitalen Geräten mit leistungsfähigen Mikroprozessoren vorbehalten.

 

Beschreibung des Asynchronmotors im feldorientierten Koordinatensystem

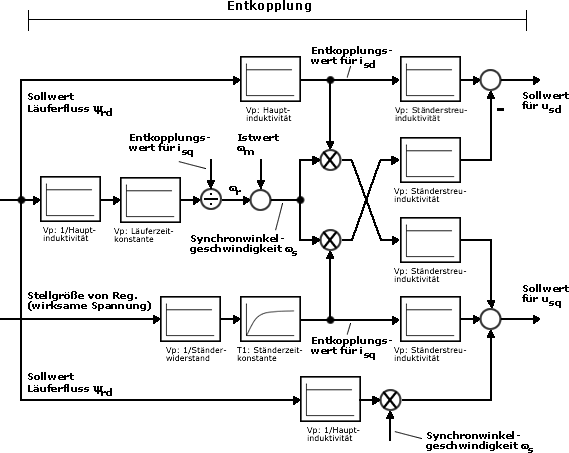
Für den Entwurf eines leistungsfähigen Stromreglers ist die Kenntnis der regelungstechnischen Struktur des Asynchronmotors unbedingt erforderlich. Deshalb wird nachfolgend der Signalflussplan des Asynchronmotors in vektorieller Beschreibung erläutert.

Die physikalischen Eingangsgrößen des Asynchronmotors sind seine Phasenspannungen. Ein Wandler bildet aus ihnen den aktuellen Zeiger der Ständerspannung. Dieser gilt für das ständerfeste Koordinatensystem und wird durch seine α- und β-Komponenten beschrieben. Für die Beschreibung im feldorientierten Koordinatensystem muss eine Übertragung des Spannungszeigers aus dem ständerfesten in das feldorientierte Koordinatensystem erfolgen. Diese Aufgabe übernimmt ein Funktionsblock, der als "Vektordreher" bezeichnet wird. Dieser Vektordreher erhält als zusätzliche Eingangsgröße eine Lageinformation, die den augenblicklichen "Verdrehungswinkel" zwischen ständer- und feldorientiertem Koordinatensystem beschreibt. Er kann so die d- und q-Komponenten des Spannungszeigers aus den α- und β-Komponenten berechnen. Der Verdrehungswinkel ergibt sich durch Integration der synchronen Winkelgeschwindigkeit. Diese setzt sich aus der mechanischen Winkelgeschwindigkeit des Läufers und einem lastabhängigen Anteil zusammen. Dieser Zusammenhang wird bei der stationären Betrachtung des Asynchronmotors durch den lastabhängig steigenden Schlupf beschrieben.

Die d- und q-Komponenten des Spannungszeigers sind die wirksamen Eingangsgrößen des Asynchronmotors. Über PT1-Glieder mit proportionaler Verstärkung rufen sie entsprechende Stromflüsse in den Ständerwicklungen hervor. Die Ständerströme gelten ebenfalls im läuferfesten Koordinatensystem und werden folglich auch als d- und q-Komponenten dargestellt. Die Stromkomponenten wirken über Proportionalglieder, in denen die Ständerstreuinduktivität als Verstärkungsfaktor auftritt, auf die Eingangsspannungen zurück. Wie im Signalflussplan zu erkennen ist, erfolgt die Rückwirkung "über Kreuz". Es tritt eine Verkopplung zwischen den Größen der d- und der q-Achse auf. Diese Verkopplung ist nicht konstant sondern nimmt mit wachsender Frequenz der speisenden Spannung zu.
Die d-Komponente des Ständerstromes bewirkt über eine PT1-Glied mit proportionaler Verstärkung die Entstehung des Läuferflusses. Das ist ein wichtiger Unterschied zum Synchronmotor, bei dem der Läuferfluss über die Permanentmagnete des Polrades erzeugt wurde.

 

Entstehung des Motordrehmomentes

An der Entstehung des Motordrehmomentes sind im Gegensatz zum Synchronmotor beide Komponenten des Ständerstromes direkt oder indirekt beteiligt. Während die q-Komponente über die Multiplikation mit einer Maschinenkonstanten direkt das Drehmoment beeinflusst, generiert die d-Komponente des Ständerstromes den Läuferfluss, der ebenfalls für die Entstehung des Drehmomentes erforderlich ist. Der Läuferfluss und die q-Komponente des Ständerstromes stehen im läuferfesten Koordinatensystem im rechten Winkel zueinander. Hier ergibt sich wieder die Analogie zum Gleichstrommotor. Dort stehen Ankerstrom und Erregerfeld ebenfalls im rechten Winkel zueinander und rufen gemeinsam das Motordrehmoment hervor. Beim Asynchronmotor muss das "Erregerfeld" nur gleichzeitig mit erzeugt werden.
Der Läuferfluss wirkt auf die q-Komponente der Ständerspannung im Sinne einer Motor-EMK zurück. Mit steigender Drehzahl des Polrades wird ein immer größerer EMK-Anteil von der q-Komponente der Ständerspannung abgezogen und die tatsächlich wirksame Spannung reduziert. Auch dieses Verhalten ist analog zum Gleichstrommotor. Änderungen des Läuferflusses wirken auf die d-Komponente der Ständerspannung zurück.

 

Stromregelung des Asynchronmotors im feldorientierten Koordinatensystem

Aus der Beschreibung des Asynchronmotors im feldorientierten Koordinatensystem ergeben sich 2 Zielstellungen für den Entwurf der Stromregelung:

1. Die q-Komponente des Ständerstromes dient als Ersatzregelgröße für die Beeinflussung des vom Motor erzeugten Drehmomentes. Die Stromregelung wirkt damit auf die q-Komponente des Ständerstromes.
2. Die d-Komponente des Ständerstromes generiert den erforderlichen Läuferfluss. Die d-Komponente des Ständerstromes muss deshalb auf einen konstanten Wert eingestellt werden, der dem Nennfluss des Asynchronmotors (bzw. seinem Leerlaufstrom) entspricht.

Als Stellgrößen dienen wie bei der Regelung des Synchronmotors die wirksamen Spannungen. Da sie rein rechnerische Größen sind, müssen sie in eine reale physikalische Spannung, die das Leistungsteil auch ausgeben kann, überführt werden. Das geschieht dadurch, dass in der Signalelektronik der Signalflussplan des Asynchronmotors einfach "rückwärts" abgearbeitet bzw. berechnet wird.

1. Entkopplung
Eingangsgrößen des Entkopplungsnetzwerkes sind der gewünschte Läuferfluss, der Sollwert der "wirksamen Spannung" in der q-Komponente (Stellgröße des Stromreglers) und die mit der Polpaarzahl des Motors multiplizierte mechanische Winkelgeschwindigkeit. Aus diesen Größen werden entsprechend dem folgenden Signalflussplan die d- und q-Komponenten der Ständerspannung und die synchrone Winkelgeschwindigkeit berechnet. Für diesen Schritt müssen die elektrischen Kenngrößen des Asynchronmotors als auch die aktuelle mechanische Winkelgeschwindigkeit bekannt sein. Die Motorkenngrößen werden deshalb während der Inbetriebsetzung des Antriebes in der Signalelektronik gespeichert. Die mechanische Winkelgeschwindigkeit wird mit einem Drehzahlgeber gemessen.

2. Koordinatenwandlung
Aus den d- und q-Komponenten des Spannungssollwertes werden anschließen die α- und β-Komponenten der Ständerspannung ermittelt. Diese Aufgabe übernimmt ein "Vektordreher", der als zusätzliche Eingangsgröße die aktuelle Lage des feldorientierten Koordinatensystems erhält. Dieser kann damit die Sollspannung aus dem läuferfesten in das ständerfeste Koordinatensystem überführen. In einem letzten Schritt wird die Ständerspannung in die 3 Phasenspannungen zerlegt und an das Leistungsteil übergeben.

Da die Stromregelung im feldorientierten Koordinatensystem arbeitet, ist es erforderlich, auch den Stromistwert in dieses Koordinatensystem zu überführen. Die Signalelektronik berechnet deshalb aus den Phasenströmen des angeschlossenen Motors die aktuelle q-Komponente des Ständerstromes.
Die Phasenströme werden nur 2-phasig erfasst, da der Strom in der dritten Phase über die Regel: "Summe der Ströme ist gleich 0" berechnet werden kann.

 

Der Stromregelkreis

Arbeiten die Entkopplung und die Koordinatenwandlung in der Signalelektronik optimal, so kompensieren sie den Koordinatenwandler und die Verkopplung im Signalflussplan des Asynchronmotors. Beide Strukturen heben sich unter dieser Bedingung auf und können in der Gesamtbetrachtung weggelassen werden. Übrig bleibt ein vereinfachter Stromregelkreis, der dem des Gleichstrommotors weitgehend gleicht. Anstelle des Ankerstromes tritt lediglich die q-Komponente des Ständerstromes auf und die Ankerspannung wird durch die "wirksame Spannung" ersetzt. Zusätzlich wird jedoch noch die Magnetisierung des Läufers, die linear in das Drehmoment eingeht, auf einen konstanten Wert eingestellt.

Der Stromregler wird typischer Weise als PI-Regler ausgelegt. Er besteht aus einem P-Glied und einem I-Glied, die parallel geschaltet sind. Die Summe der Ausgangssignale ergibt die Sollspannung.

Das P-Glied und das I-Glied übernehmen unterschiedliche Aufgaben im Stromregler:

• Das P-Glied dient zur unverzögerten Reaktion auf Sollwertänderungen bzw. das Einwirken von Störgrößen. Treten aufgrund dieser Vorgänge Regelabweichungen auf, bewirkt das P-Glied eine sofortige Änderung der wirksamen Spannung und damit eine unverzögerte Reaktion des Stromreglers. Das P-Glied ist damit für die Dynamik der Stromregelung entscheidend.
• Das I-Glied dient zur Kompensation von stationären Störgrößen. Solche Störgröße treten z. B. aufgrund nicht optimaler Entkopplungen und Koordinatenwandlungen auf.

Die Verwendung eines PI-Reglers ist mit dem Nachteil verbunden, dass dynamische Regelvorgänge im Stromregelkreis immer mit einem Über- bzw. Unterschwingen des Stromistwertes verbunden sind. Durch entsprechende Wahl der Reglerparameter muss ein Kompromiss zwischen einer hohen Dynamik und einer akzeptablen Überschwingweite gefunden werden. Bei der Optimierung des Regelkreises ist zu beachten, dass die auftretenden elektrischen Größen "mathematische" Größen darstellen und im Gegensatz zu einem Gleichstrommotor nicht direkt gemessen werden können. Für die Beobachtung dieser Größen sind entsprechende D/A-Wandler in der Signalelektronik oder integrierte digitale Aufzeichnungsfunktionen (Trace) erforderlich.

Hinweis:
Die Begrenzung der Ständerspannung wurde zum Zwecke der Vereinfachung nicht dargestellt. In der praktischen Realisierung muss sie jedoch berücksichtigt werden. Im allgemeinen wird deshalb bei Eintritt des Spannungssollwertes in die Begrenzung das I-Glied angehalten und so ein starkes Aufintegrieren der Regelabweichung vermieden.

 

Motor-EMK

Eine separate Vorsteuerung der Motor-EMK ist im Gegensatz zur Stromregelung beim Gleichstrommotor nicht erforderlich. Die Wirkung der Motor-EMK wurde in der Entkopplung bei der Berechnung des Sollwertes für die q-Komponente der Ständerspannung bereits berücksichtigt.